Dersom vi fester et tau til en gjenstand og drar, så påfører vi en kontaktkraft på gjenstanden. Tauet får en strekkraft F_tau og kraftens retning sammenfaller med tauretningen. Tauet påfører en like stor og motsatt rettet kraft i den andre enden. Her skal vi anta at tauets egenvekt er mye mindre enn strekket og da blir tauet rettlinjet og strekket blir konstant. Tauet fungerer son en aksialstav. Tau, kjettinger og kabler er konstruksjonselementer som bare kan overføre strekkrefter og som gjerne regnes fri for bøyemotstand. Hva skjer f.eks. om du prøver å bøye en kjetting?

Tau skiller seg fra andre konstruksjonselementer ved at den geometriske formen påvirkes av belastningen som virker på tauet. En trinse er et hjul med spor som brukes for å endre tauretningen. Så lenge trinsen kan rotere fritt vil strekket være det samme på hver side av trinsen. Figuren viser en trinse hvor det er ført et tau over. På hjulet virker F_tau og G, og i akselen i senteret C virker en opplagerkraft. Moment­likevekt om senterpunket gir:

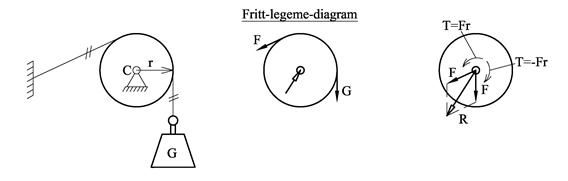
Når vi fører et tau over en trinse så beholder strekkraften i tauet målet, men kraften skifter retning. Retningsendringen gir en kraft på trinsen tilsvarende resultanten av de to taukreftene. Resultanten angriper i senterpunktet. Et blokkarrangement som vist under kan dermed erstattes av denne resultanten.

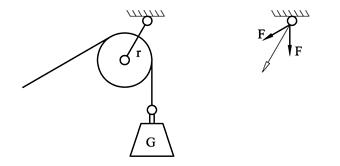
Figuren under oppsummerer det vi har lært. Legg merke til at opplagerkraften blir større jo skarpere vinkel tauet får over hjulet.

Taljer

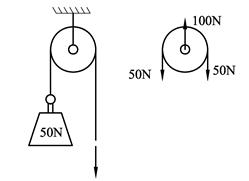
Figuren viser en trinse som er festet i taket og som brukes for å løfte et lodd. Når vi skal finne taukrefter og krefter i opplageret setter vi opp et fritt-legeme-diagram for trinsen. Det virker to like store taukrefter på trinsen og disse virker i samme retning. Dermed blir kraften på festet i taket dobbelt så stor!

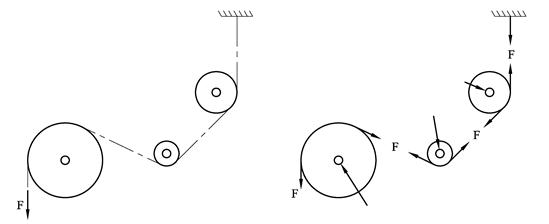
Neste figur viser et løftearrangement med to trinser. Likevekt av nedre trinse viser at trekkraften reduseres til det halve, dvs F_tau = G/2, og dette kan vi dra nytte av. Kraften på takfestet blir F_tak = 1,5G.

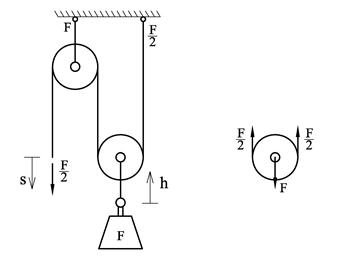
Vi skal nå gjøre en energibetraktning av løftearrangementet. Fra fysikk har vi lært at utført arbeid er lik tilført energi, og utført arbeid = Kraft × Forflytning i kraftens retning, dvs W = F·s. Hvis vi ser bort fra friksjon og kinetisk energi så får vi at Utført arbeid = Tilført potensiell energi, dvs F_tau · s = G · h

Likningen forteller oss at når F_tau er halvparten av G så må veilengden s være dobbelt så stor som løftehøyden h. Vi har altså oppnådd en halvering av taukrafta mens veilengden for å løfte loddet blir doblet. Det vi vinner på kraftsiden taper vi gjennom økt veilengde. Et slikt arrangement kalles for en toskåren talje. Legg merke til at hva som er utført arbeid og hva som er tilført potensiell energi er en definisjonssak og vi kan like gjerne snu om på begrepene. Figuren til venstre under viser en firskåren talje hvor taukraften reduseres til ¼ mens veilengden firedobles. Hva slags talje har vi til høyre?

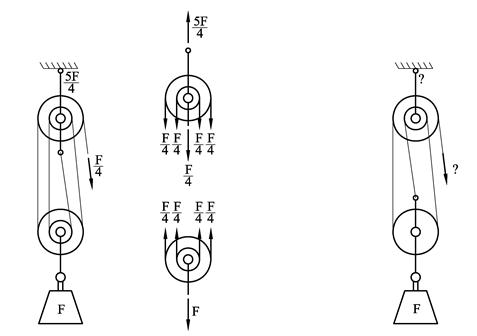
Utveksling

Taljer er et eksempel på et fenomen som kalles for utveksling. Vi har mange ulike former for utveksling. Figuren under viser en vektstang som kan brukes for å løfte tunge gjenstander:

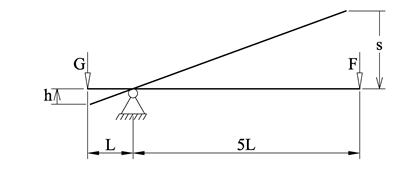
Vi kan enkelt sette opp momentuttrykk som viser at F=G/5. Alternativt kan vi sette opp energilikningen . Ut fra geometrien ser vi at s = 5h, og da blir F=G/5.

Til sist skal vi se på et løftearrangement hvor to tau er viklet rundt hvert sitt hjul.

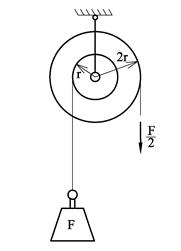
Vi setter opp momentlikning om senterpunktet. Kraften halveres mens veilengden dobles. Vi sier at vi har en utveksling på 2:1.