Fram til nå har vi konsentrert oss om å bestemme reaksjonskrefter i opplagrene. Vi skal nå se hvordan vi kan kartlegge hvilke krefter og momenter som virker inni en bjelke, og vi begynner med normalkraften.

Normalkraft

Figuren over viser en bjelke som er fastholdt i en ende og hvor det virker en strekkraft i den andre enden. Ut fra likevektslikningene skjønner vi at det må virke en like stor og motsatt rettet reaksjonskraft i den fastholdte enden. Vær obs. på at selv om de to kreftene er like stor og motsatt rettet så er de ikke motkrefter til hverandre.

 

Og hva skjer inni en strekkbelastet bjelke? For å synliggjøre de indre kreftene må vi tenke oss at bjelken deles i to der hvor vi ønsker å bestemme de indre krefter. Det er i prinsippet det samme vi gjør som når vi tegner fritt-legeme-diagrammer. I figuren over er bjelken snittet på tvers på et vilkårlig sted. For at venstre halvdel skal være i likevekt må det finnes en strekkraft N, og for at høyre halvdel skal være i likevekt må det også finnes en strekkraft N her, og disse to kreftene er like store og motsatt rettet fordi de er motkrefter og således tilhører de hverandre. Det er disse kreftene som gjør at bjelken holder seg sammen når den strekkes. Det virker altså strekkrefter i hele bjelkens lengde og dette kan illustreres som vist i figuren under. Man kan tenke seg at de to endekreftene vandrer gjennom bjelken.

De indre kreftene vi finner i bjelker kalles gjerne for snittkrefter og snittkraften N kalles for normalkraft fordi den virker normalt på snittet.

Eksempel

Kartlegg normalkreftene i bjelken som er belastet med diverse krefter i bjelkens lengderetning. Bjelken er i likevekt.

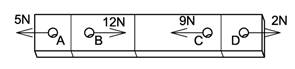
Vi deler bjelken i to et vilkårlig sted mellom A og B. Likevekt av venstre halvdel tilsier at det i snittet virker 5N mot høyre. Alternativt kan vi sette opp likevektslikning av høyre halvdel som også gir en snittkraft på 5N, denne gang mot venstre (ΣF_x = 0 gir 12-9+2-N = 0 gir N_x =5). Vi står altså fritt til å bruke hver av de to halvdelene for å bestemme snittkreftene og vi velger gjerne den halvdelen som gir det enkleste regnestykket.

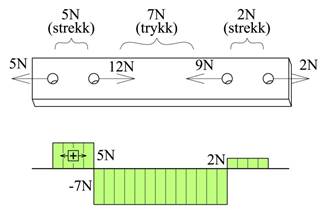
På tilsvarende vis kan vi bestemme strekkraften mellom B og C som -7N, dvs. her får vi trykkraft og det betyr pilene må snues.

Mellom C og D kan vi bruke høyre halvdel og da ser vi umiddelbart at vi får strekket 2N. Legg merke til at alle snitt er vilkårlig plassert mellom punktlastene og det betyr at normalkraften har konstant verdi for hvert intervall.

Strekk- og trykkrefter kalles for normalkrefter fordi disse kreftene virker normalt på bjelketverrsnittet, og vi kan oppsummere resultatene over i et såkalt normalkraftdiagram. Her er selve bjelken vist kun som en strek og så vises normalkraften som en funksjon av posisjonen.

Bøyemoment og skjærkraft

Figuren over viser en såkalt utkragerbjelke hvor det virker en kraft på skrå i høyre ende. Vi legger inn et koordinatsystem hvor x-aksen sammenfaller med bjelken, og ved hjelp av likevektslikningene kan vi bestemme fastholdingskreftene F_x, F_y, og momentet M_z i venstre ende.

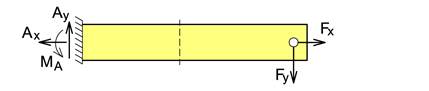
På tilsvarende vis kan vi bestemme krefter som finnes inni bjelken. Vi tenker vi oss at bjelken deles i to der hvor vi ønsker å bestemme de indre kreftene. For at høyre halvdel skal være i likevekt i lengderetningen må det virke kraften N normalt på snittet. På tilsvarende vis må det virke en skjærkraft V som ligger i selve snittet for å skape likevekt på tvers av bjelken.  Men fordi F_y og V ikke ligger på linje dannes det et kraftpar som skal rotere høyre halvdel med klokken. For å holde igjen rotasjonen må det i tillegg virke et moment M i snittet. Om vi i stedet satt opp likevektslikninger for venstre halvdel så ville vi få akkurat de samme snittkreftene, men denne gang med motsatt fortegn og dette skyldes at snittkreftene som er på hver halvdel er motkrefter til hverandre.

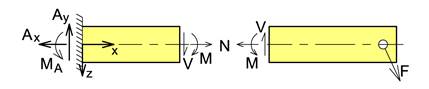
Generelt vil vi ha følgende snittkrefter; en normalkraft N som virker i bjelkens akseretning, en skjærkraft V som virker på tvers av bjelkeaksen og et bøyemoment M som virker i belastningsplanet. Snittkreftene er indre krefter som opptrer parvis som krefter og motkrefter på hver sin side av tverrsnittet. I og med at kraft og motkraft virker hver sin vei, blir fortegnsreglene litt kompliserte. Hvis vi legger inn et koordinatsystem som vist under skal positiv N virke i positiv x-retning, positiv V virke i z-retningen og positiv M virke om y-aksen jf. høyrehåndsregelen.

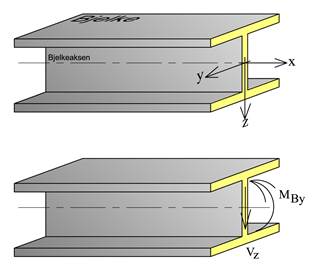
Dersom bjelken er horisontal og x-aksen går fra venstre mot høyre får vi positive retninger for N, V og M som følger.

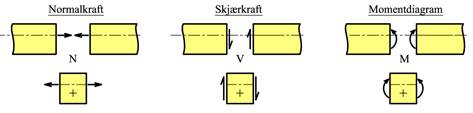
Normalkraften N er positiv når den gir strekk i bjelken.

Skjærkraften V er positiv når den roterer elementet med klokken.

Bøyemomentet M er positivt når bjelken får strekk på bjelkens underside.

Det er snittkreftene som gir en belastning på bjelkematerialet og vi er derfor interessert i å finne de største snittkreftene i bjelken. Snittkreftene varierer langs bjelken og vi skal lære hvordan vi kan lage momentdiagram, skjærkraftdiagram og normalkraftdiagram som gir en god oversikt over snittkreftene.

Bjelkens differensiallikning

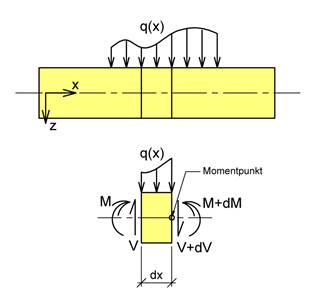
Figuren viser en bjelke som er belastet med en generell fordelt last q(x) og vi ser på kreftene som virker på et lite bjelkeelement med lengden dx.

Tverrlasten q(x) er altså den deriverte av skjærkraften, som igjen er den deriverte av bøyemomentet. Resultatene over kan oppsummeres i bjelkens differensiallikning

Alternativt kan vi sette opp følgende uttrykk for bøyemomentet.

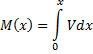
Vi er spesielt interessert i å kartlegge de indre momentene og vi skal legge merke til følgende viktige følger av bjelkens differensiallikning. Endringen i moment fra posisjon x₁ til posisjon x₂ tilsvarer arealet under skjærkraftdiagrammet mellom posisjon x₁ og x₂. Videre vil skjærkraftdiagrammet er lik null der hvor momentdiagrammet har topp- og bunnpunkt.

M- og V-diagrammene

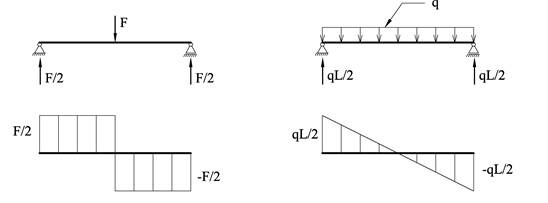
Figuren under viser hvordan V- og M-diagrammet ser ut for jevnt fordelt last. Legg merke til at V = 0 på midten hvor M har sin maks-verdi

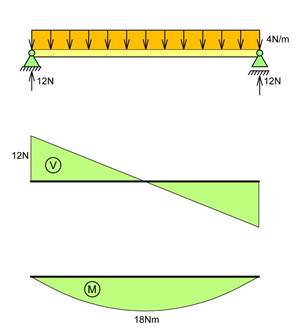
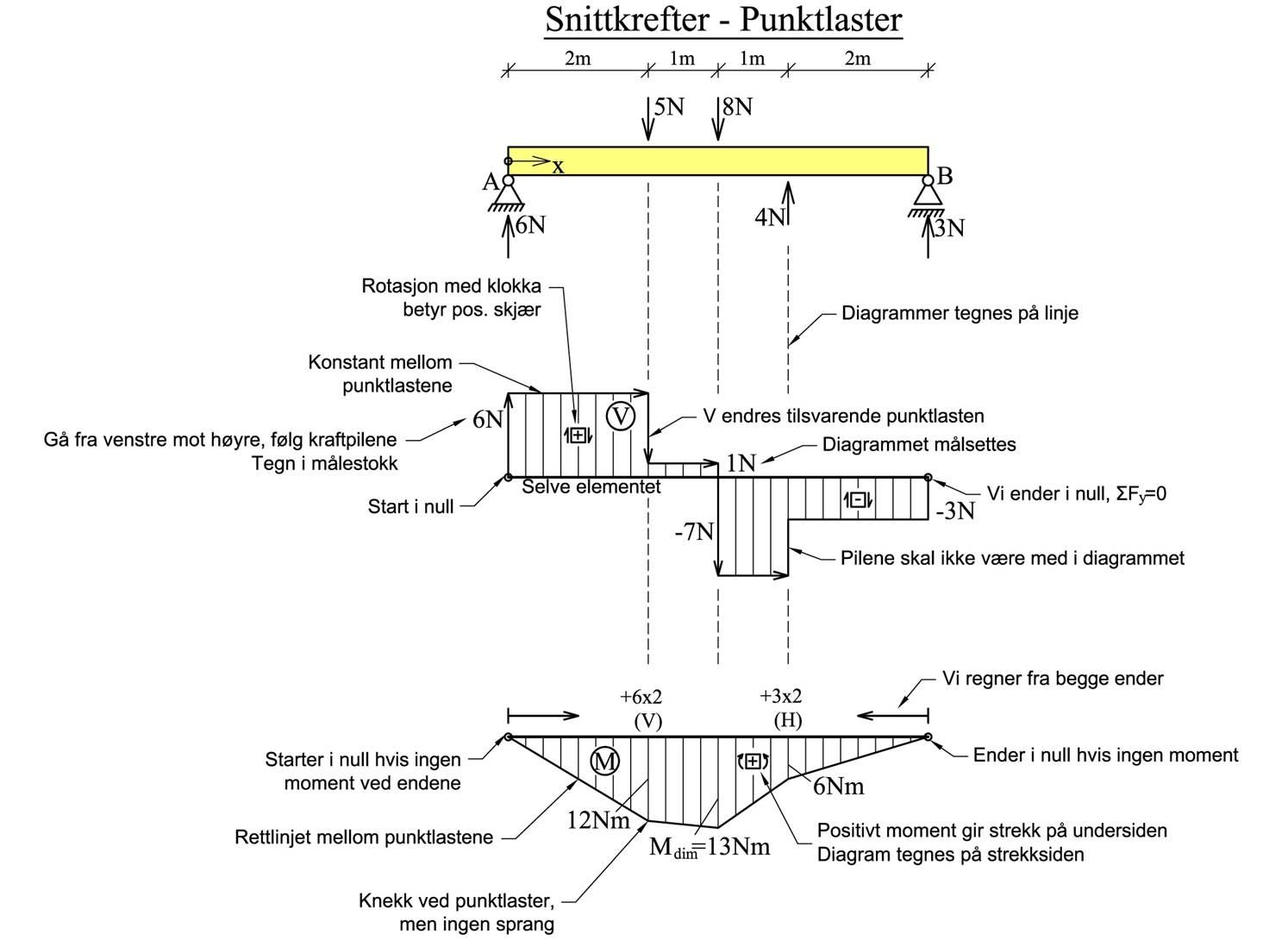
Dersom vi i stedet beskriver lasten som en rekke punktlaster blir diagrammene som følger.

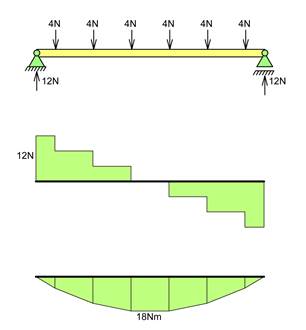
Alle belastninger virker over en viss utstrekning. Figuren under viser hvordan V- og M-diagrammet påvirker av hvor stort område belastningen fordeles over. Punktlast gir typisk størst M og det er dermed konservativt å bruke punktlaster.

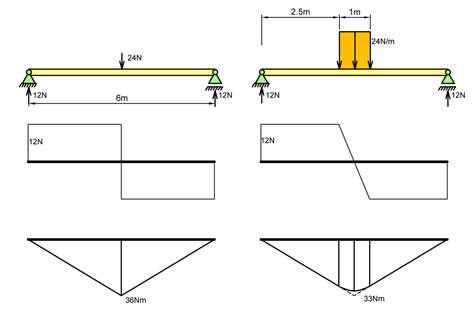
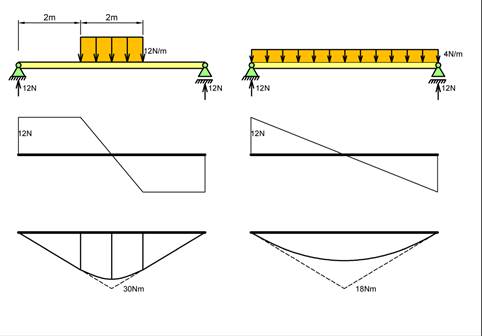
Vi skal se hvordan vi kan bruke arealer under skjærkraftdiagrammet for å finne det dimensjonerende bøyemoment for to viktige lasttilfeller.

Figurene under oppsummerer det meste vi bør vite om skjærktaftdiagrammet og bøyemomentdiagrammet. Studer disse nøye.