De fleste problemstillinger som skal løses i mekanikkfaget begynner med å bestemme reaksjonskreftene, dvs. de kreftene som oppstår der hvor konstruksjonen holdes fast. Vi skal her presentere en prosedyre som vi kan bruke for å bestemme de ukjente reaksjonskrefter. Vi skal stort sett følge denne prosedyren, men av og til blir prosedyren omstendelig og vi kan gjerne gjøre forenklinger.

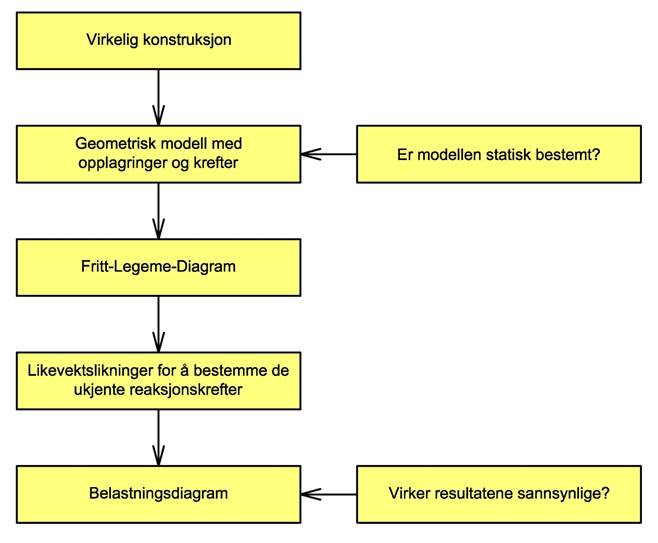
Formålet med å bestemme reaksjonskreftene er at vi vil ha full oversikt over alle krefter som virker på konstruksjonen før vi går videre og løser vårt mekanikkproblem. Vi skal nå illustrere metodikken med eksempelet under hvor vi skal gjøre beregninger på en såkalt løpekattbjelke.

 

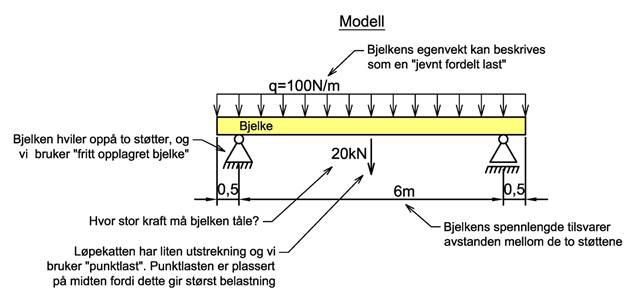
Mekanikk handler om virkelige konstruksjoner, men for at beregningene ikke skal bli alt for kompliserte må vi gjøre noen antakelser og forenklinger. Vi lager en modell av konstruksjonen som inneholder den informasjon vi behøver for å kunne gjøre våre beregninger. Modellen må beskrive den geometriske utformingen av konstruksjonen og den må beskrive kreftene som virker på konstruksjonen. Hvilke dimensjoner har konstruksjonen? Hva skal tas med i modellen? Vi kan ikke ta med alle detaljer og vi må avgrense modellens utstrekning. Der modellen stopper, må vi velge opplaginger som sier noe om hvordan konstruksjonen forholder seg til omgivelsene. Vi må vite hvor store krefter som virker på konstruksjonen, hvordan kreftene fordeler seg (skal vi bruke punktlast eller jevnt fordelt last), hvor kreftene virker og hvilken retning de har. Er det flere krefter på konstruksjonen og virker disse samtidig? Må vi ta hensyn til konstruksjonens egenvekt? De ytre kreftene kan variere mye og vi baserer gjerne våre beregninger på de største tenkelige kreftene og med den ugunstigste plasseringen, slik at vi er på den sikre siden. Å lage en modell som beskriver den virkelige konstruksjonen på en tilfredsstillende måte kan være vanskelig og krever gjerne en del erfaring. Figuren under viser en modell av bjelken som er vist på bildet over.

 

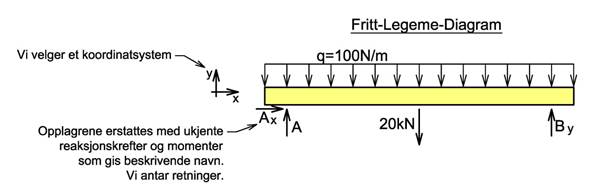
Vi kontrollerer om modellen er statisk bestemt modell slik at vi kan løse problemet ved hjelp av likevekts­likningene. Vi tegner et fritt-legeme-diagram hvor alle opplagringer erstattes med ukjente reaksjonskrefter. Vi velger et koordinatsystem og reaksjonskreftene gis navn, f.eks. A_x, A_y og M_A. Sammensatte konstruksjoner deles opp ved ledd og ved stive forbindelser.

Vi bruker likevektslikningene for å bestemme de ukjente reaksjonskreftene og presenterer våre beregninger i et belastningsdiagram. I belastningsdiagram tegnes både de ytre kreftene og reaksjonskreftene, og kreftene tegnes med riktig retning og krefter som er lik null tas ikke med. Til slutt ser vi over resultatene og vurderer om beregningene virker sannsynlige. Er det like mye kraft som virker oppover som nedover osv? Belastningsdiagrammet danner utgangspunkt for de videre beregningene.

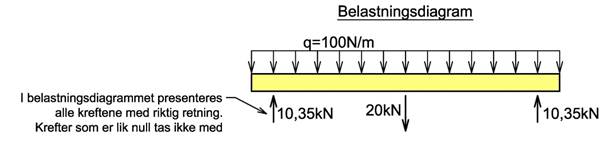
Når de ukjente opplagerkreftene er bestemt presenterer vi resultatene i et såkalt belastnings­diagram (BD) som viser samtlige krefter som virker på konstruksjonen. BD er temmelig likt FLD, men det er satt inn verdier for de ukjente størrelsene. Vær obs. på at krefter som er lik null ikke skal tas med og at alle krefter skal tegnes med rett kraftretning. Dersom man regner seg fram til en negativ kraft så skal pilen alltid snus.

BD gir det totale bildet av belastningene på konstruksjonen og man bør alltid gjøre en vurdering av om resultatene i belastningsdiagrammet virker troverdige. Likevekts­likningene kan betraktes som et kraftregnskap, dvs. at det skal virke like mye krefter oppover som nedover og like mye krefter mot høyre som mot venstre. Vi avslutter gjerne oppgaven med å sjekke kraftregnskapet.