Et sentralt begrep i mekanikk er momentet, som litt forenklet forklares som “kraft ganger arm”. Momentet er en enkel metode for å beregne krefters beliggenhet. Momenter har mange likhetstrekk med de fysiske kraftparene, og det er ikke uvanlig at disse begrepene brukes om hverandre. Men momentet er egentlig bare et regnehjelpemiddel uten noen fysisk betydning.

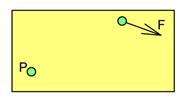
Legemet under er belastet med kraften F. Figuren viser momentpunktet som har fått navnet P. Alle moment­beregninger begynner med at man velger seg et momentpunkt, og momentpunktet er ikke annet enn et referansepunkt med kjent beliggenhet.

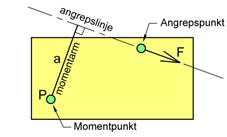
Kraftens “moment om P” er definert som M_p = F×a, hvor F er kraftens mål og a er lengden av kraftens momentarm. Momentet har enheten Nm. Momentarmen er avstanden mellom momentpunktet og kraftens angreps­linje, og momentarmen skal stå normalt på angrepslinjen, se figur under. Det er spesielt momentarmen som kan være litt vanskelig å forstå.

Slik momentarmen er definert blir momentet avhengig av momentpunktets beliggenhet, og vi må derfor alltid fortelle hvor momentpunktet ligger. Momentet om punkt A angis som M_A osv. Vi kan plassere momentpunktet hvor som helst, det kan til og med ligge utenfor legemet. Men så lenge vi arbeider med plane kraftsystemer må momentpunktet ligge i dette planet. Det kan være litt krevende å bestemme momentarmen fordi vi først må finne ut hvor normalen fra momentpunktet treffer angrepslinjen, og dette er bare et matematisk punkt.

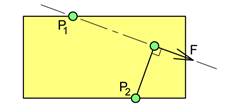
Vi står fritt til selv å velge momentpunktet, men det er noen smarte momentpunkter som gjør beregningene enklere. Vi skal se på et par spesialtilfeller. Fordi momentpunktet P₁ ligger på kraftens angrepslinje så blir momentet lik null. Og vi kjenner momentarmen fra P₂ fordi denne treffer i kraftens angrepspunkt.

Når kreftene er horisontale eller vertikale, og når krefter sammenfaller med legemets geometri så finner vi enkelt momentarmen.

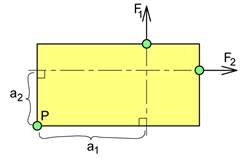
Hvis vi innfører et koordinatsystem, kan vi dekomponere alle krefter x- og y-retninger og bestemme momentarmen for hver komponent, og dette er veldig vanlig. Legg merke til at krefter i x-retning hører sammen med momentarmer i y-retning og vice versa.

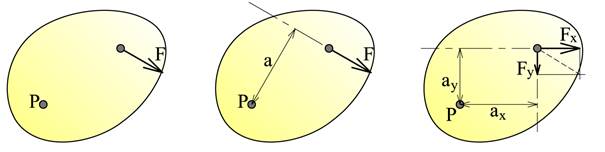
Momentet på to måter

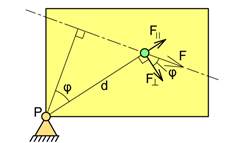
I figuren under har vi trukket en linje mellom momentpunkt og kraftens angrepspunkt. Vi dekomponerer kraften i en komponent F_^ som står vinkelrett på denne linjen og en komponent F_|| som er parallell med linjen. Legg merke til at det kun er F_^ som gir moment, og vi kan sette M_P = F·a = F_^·d. Dette er en alternativ og likeverdig måte å bestemme momentet på.

At vi har to likeverdige alternativer for momentet kan vises med følgende figurer:

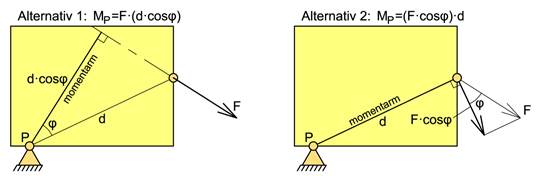
Hvis vi flytter en kraft langs angrepslinjen så vil momentet ikke bli påvirket. Dette skyldes at momentarmen kun refererer til selve angrepslinjen.

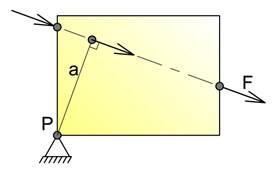
Legg merke til hvordan F_^ og forandrer seg når vi flytter kraften langs angrepslinjen, men M_P forandrer seg altså ikke.

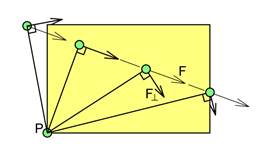
Moment er “kraft ganger arm” og samme moment kan oppnås med stor kraft og liten arm eller med liten kraft og stor arm. Kraftens orientering har heller ingen betydning.

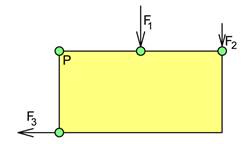
Figur 1 Tre krefter som gir samme moment om P

Dreieretning

Momenter har et mål og momenter har en dreieretning. For å forstå hva vi mener med momentets dreieretning så kan vi forestille oss at legemet er fastholdt med en aksling i momentpunktet, og så spør vi; “vil kraften føre til at legemet roterer med klokka eller mot klokka”? Med dreieretning mener vi dreieretning i forhold til momentpunktet og det betyr at en og samme kraft kan gi forskjellig dreieretning avhengig av momentpunktets beliggenhet i forhold til kraften, dvs. hvilken side av angrepslinjen momentpunktet ligger.

 

Dreieretning er viktig fordi momenter som virker i samme retning forsterker hverandre mens momenter med motsatt dreieretning motvirker hverandre. Vi bruker gjerne fortegn for å angi dreieretningen, og da kan vi f.eks. velge “med klokka” som positiv dreiretning. Momenter som virker “mot klokka” skal da ha negativt fortegn. Vi kan gjerne bruke symbolene P og Q for å angi positiv dreieretning.

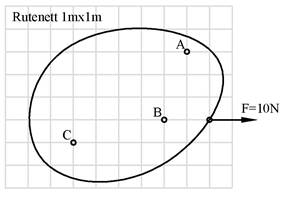
For legemet under velges P, dvs. “med klokka” som positiv dreieretning og vi får PM_A = -30Nm (mot klokka) og PM_C = +10Nm (med klokka). Hvis “mot klokka” er positiv dreieretning får vi motsatte fortegn, dvs. QM_A = +30Nm og QM_C = -10Nm. Legg også merke til at M_B = 0 Nm.