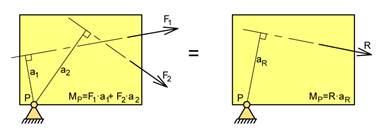
Momentsetningen for plane kraftsystemer
Resultantens moment om et vilkårlig punkt P er lik summen av enkeltkreftenes momenter om P.
R·aR = Σ(Fi·ai)
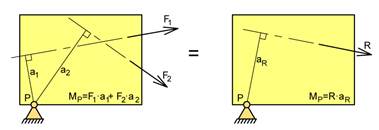
Momentsetningen gir oss sammenhengen mellom resultantens moment og enkeltkreftens momenter. Momentsetningen følger direkte av parallellogramloven og er ikke en egen lov, men den kan gjøre en del beregninger i mekanikk mye enklere. Vi har tidligere lært hvordan vi bestemmer resultanten for et kraftsystem f.eks. med kraftpolygonet, men her får vi bare mål og retning for resultanten. Med momentsetningen kan resultantens beliggenhet beregnes som aR = Σ(Fi·ai)/R.
Når vi summerer momenter er det slik at momenter med samme dreieretning forsterker hverandre mens momenter med ulik dreieretning motvirker hverandre. Vi bruker fortegn for å holde orden på dreieretning. I tilfellet under velger vi “med klokka” som positiv dreieretning og resultantens moment blir PΣMP = F1a1 – F2a2. Hvis PΣMP blir positivt så skal også R ha dreieretningen “med klokka”.

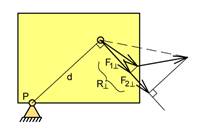
Figuren viser et legeme hvor det virker to vilkårlige krefter F1 og F2. Målet er å sette opp et uttrykk for resultantens moment om punktet P.
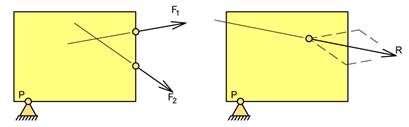
Resultanten konstrueres ved hjelp av parallellogramloven. Flytter både F1, F2 og R langs sine angrepslinjer slik at alle kreftene angriper i skjæringspunktet. Resultantens moment om P kan enten uttrykkes som R·aR eller som R^·d, se figur under. Tilsvarende kan momentene fra F1 og F2 uttrykkes som F1^·d og F2^·d. Moment fra hver kraft kan uttrykkes på to alternative måter: R·aR = R^·d, F1·a1 = F1^·d og F2·a1 = F2^·d.
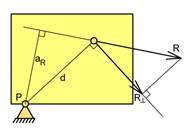
Vi ser av figuren under at R^ = F1^ + F2^ og vi kan sette R^·d = (F1^+ F2^)·d. Løser opp parentesen og vi får R^·d = F1^·d + F2^·d. Erstatter hvert ledd med standard momentuttrykk og får R·aR = F1·a1 + F2·a2.
Dermed har vi utledet momentsetningen ut fra parallellogramloven. Sammenhengen er vist for to krefter, men vi kan vise at momentsetningen gjelder for resultanten av alle plane kraftsystemer, uansett hvor mange krefter som inngår og uansett valg av momentpunkt.