
Det er mulig å bestemme resultanten av et kraftsystem grafisk ved å tegne en kraftpolygon, og den grafiske metoden er nyttig fordi den gir en god forståelse av kraftbildet, men den blir gjerne upraktisk når kraftsystemet blir komplisert. Vi skal se på den analytiske metoden hvor vi bestemmer resultanten ved hjelp av regning.
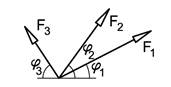
Figuren viser et kraftsystem som består av tre krefter. Vi kjenner kreftenes mål og retning og vi skal bestemme resultanten. Vi begynner med å velge oss et passende koordinatsystem og dekomponerer alle krefter i x-retningen og y-retningen, dvs. kraften F1 erstattes med to komponenter F1x og F1y osv. Alle x-komponentene kan nå uten videre legges sammen så lenge vi passer på fortegn, og vi finner resultantens x-komponent Rx. På tilsvarende vis finner vi Ry ved å legge sammen alle y-komponentene. Når vi skal beregne Rx og Ry så kan det være lurt å velge seg positive retninger f.eks. ® og . Alle komponenter som virker med pilretningen skal ha positivt fortegn mens krefter som virker mot pilretningen skal ha negativt fortegn. Hvis blir summen av f.eks. x-komponentene blir negativ så betyr det at Rx går mot venstre. For kraftsystemet over beregner vi Rx og Ry som følger:
![]()
![]()
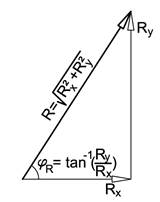
Når vi har funnet Rx og Ry kan resultantens mål R bestemmes med Pytagoras. Resultantens retning jR bestemmer vi ved hjelp av tangens.
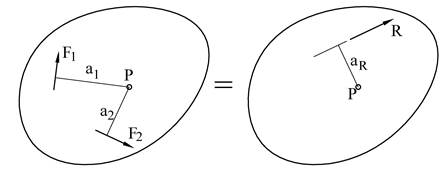
Får å bestemme resultantens beliggenhet bruker vi momentsetningen som er behandlet i eget kapittel. Momentsetningen sier at resultantens moment om et fritt valgt referansepunkt P er lik summen av enkeltkreftenes momenter om P, dvs. R· aR = Σ(Fi · ai).
I mekanikk er det viktig å tegne gode figurer som viser kreftenes retning og beliggenhet, men når vi arbeider analytisk blir kravet til figurens nøyaktighet naturligvis ikke det samme som når vi jobber grafisk.
Den analytiske metoden for å bestemme resultantens mål og retning går som følger:
- Fastlegg mål, retning og angrepslinjens beliggenhet for alle
kreftene.
- Velg x- og y-retning og dekomponer hver kraft i x- og
y-retningen.
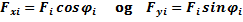
- Velg positive retninger og adder komponentene. Pass på fortegn.
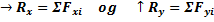
- Resultantens mål bestemmes med Pytagoras mens retningen
bestemmes med tangens. Pass på hvilken kvadrant resultanten ligger i.
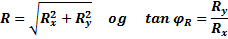
- Resultantens beliggenhet bestemmes med momentsetningen.
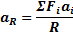
- Svaret presenteres i figur hvor kraftens retning og beliggenhet framkommer på en entydig måte.


