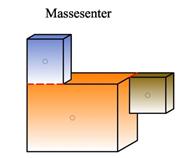
Med begrepet tyngdepunkt mener vi punktet hvor resultanten til legemets tyngdekrefter angriper. Resultantens angrepslinje går gjennom dette punktet uansett hvordan legemet er orientert i forhold til tyngdefeltet. Tyngdepunktet kalles også for massesenteret.

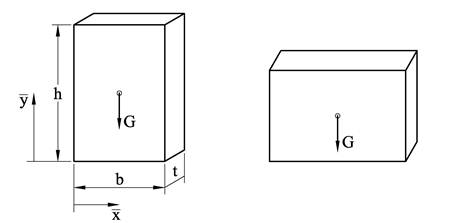
For legemer med enkel geometri og med homogent materiale, dvs. samme materialegenskaper i hele legemet, bestemmer vi tyngdepunktets plassering kun utfra geometrien. For en firkantet kloss får vi f.eks.:

Tyngdepunktets plassering angis alltid i forhold til et fritt valgt referansepunkt. I Meccanica angis tyngdepunktet med en strek.

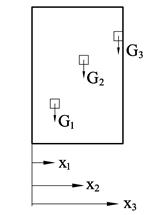
Egentlig er tyngden fordelt utover hele materialet; på hver liten partikkel i legemet virker det en liten kraft og legemets tyngde er kraftresultanten av G₁, G₂ osv. I og med at de fordelte kreftene er parallelle, kan vi addere disse sammen uten videre og finne tyngden som. Tyngdens beliggenhet bestemmes med momentteoremet som sier at resultantens moment skal være lik summen av enkeltkreftenes momenter om ethvert punkt, dvs. .

Tyngden kan uttrykkes ved materialets egenvekt og legemets volum, G = ρgV. Vi setter opp den viktige tyngdepunktsetningen som brukes for å bestemme tyngdepunktets beliggenhet. Det er også tatt med et generelt uttrykk hvor tyngdepunktet bestemmes ved å integrere over hele volumet. Tilsvarende uttrykk kan settes opp for

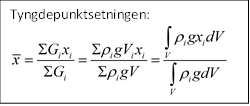
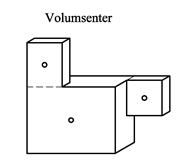
Vi ser at tyngdens akselerasjon kan reduseres bort, og det betyr at det ikke spiller noen rolle om vi regner i kg eller i N. Hvis legemet kun består av ett materiale, dvs. at materialet er homogent, kan også egenvekten reduseres bort og tyngdepunktet kan bestemmes utelukkende ut fra legemets volumgeometri. Vi definerer volumsenter som følger:

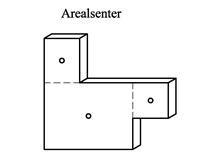
Hvis legemet i tillegg har konstant tykkelse kan tyngdepunktet bestemmes utelukkende ut fra arealberegninger og vi betrakter legemet to-dimensjonalt. Vi definerer arealsenter som følger:

I mekanikk gjør vi gjerne arealberegninger for å bestemme resultanten av krefter som er jevnt fordelt over en flate, og resultantens beliggenhet sammenfaller da med arealsenteret.