Oppgave

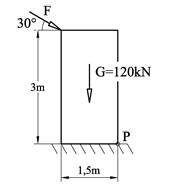
Figuren viser en kloss hvor det virker en skråkraft. Beregn største tillatte kraft når sikkerhetsfaktoren i forhold til glidning skal være n_F = 1,5. μ = 0,25 mellom kloss og underlag.

Løsning

Normalkraft på kontaktflaten:   F_N = 120 + Fsin30°

Friksjonskraft:                            F_F = Fcos30°

Klossen glir hvis F_F = μF_N :      

F_tillatt = F_gli / 1,5 = 27,0kN

Oppgave

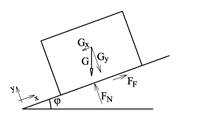
Figuren viser en kloss som ligger på en skrå flate. Ved hvilken vinkel vil klossen begynne å gli?

Løsning

Friksjonsoppgaver handler om å bestemme krefter som virker parallelt med et glideplan og normalt på et glideplan. Det er derfor hensiktsmessig å legge inn et koordinatsystem på skrå som vist på figuren.

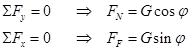
Klossen glir hvis F_F = μ_oF_N, dvs.  

Oppgave

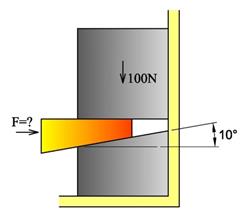
I dette eksempelet skal vi se på hvordan vi kan bruke kile som løfteredskap. Ved å dytte inn kilen som vist under vil den øvre klossen løfte seg, men samtidig oppstår det friksjon på to gildeflater som må overvinnes. Hvor stor kraft må til for å dytte inn kilen? Vil kilen gli ut igjen hvis kraften F fjernes? Friksjonstallet er oppgitt til μ = 0,2.

Løsning

Vi begynner med å se på øvre kloss:

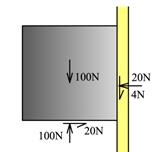
Det virker 100N mellom kile og øvre kloss og når kilen sklir får vi her friksjonskraften 0,2·100 = 20N. Klossen trykkes mot bakveggen og vi får en ny glideflate. Hvis vi antar samme friksjonstall mot bakveggen får vi en friksjonskraft på 0,2·20=4N som gir en økning i normalkraften mot kilen. Her må vi altså iterere oss fram til en løsning. Det er nokså vanlig at man ser bort fra slike sekundære virkninger i friksjonsoppgaver. Kreftene fra kilen mot øvre kloss virker også som motkrefter på kilen.

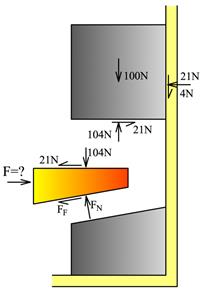
I det klossen sklir får vi:   (glidekriterium, ikke likevektslikning)

Likevekt av kilen:

Vi bruker kraften 61N for å løfte 100N. Vi har altså fått en form for utveksling. Beregningene er presentert under. Vi kan forenkle beregningene og oppnå tilnærmet samme svar.

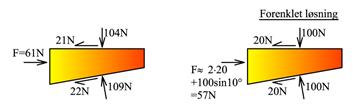
Vil klossen gli ut igjen når vi fjerner kraften F? Glideflaten vil være under kilen. Figuren under viser hvordan F_F og F_N forholder seg til hverandre. Beregner friksjonsvinkelen:

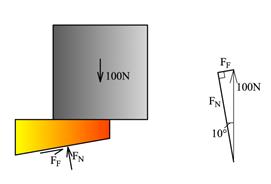
Skråplanet har vinkelen 10° og kilen glir følgelig ikke ut.

Oppgave

Tre stålrør er stablet oppå hverandre som vist under. Hvor stort friksjonstall må vi ha mellom rør og underlag for at stabelen ikke skal ramle sammen? Anta at kraften mellom rørene virker normalt på kontaktflaten.

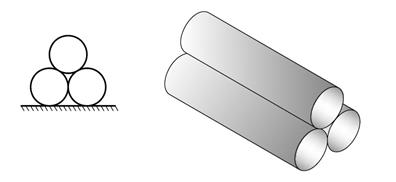
Løsning

Tegner fritt-legeme-diagram for hvert rør:

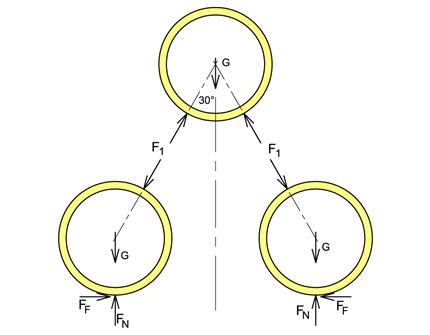
Likevekt av øvre rør:

Likevekt av nedre rør:

Røret glir ut hvis F_F overskrider F_F,maks