Eksempel (kombinert belastning)

Tegn V- og M-diagram

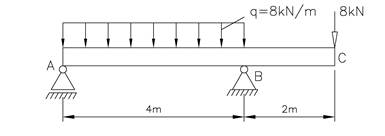
Løsning

Først må vi bestemme reaksjonskreftene som presenteres i et belastningsdiagram:

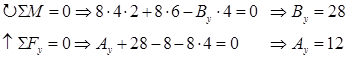
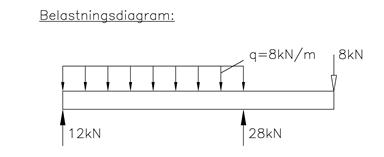
Vi begynner med å finne uttrykk for snittkreftene mellom A og B.

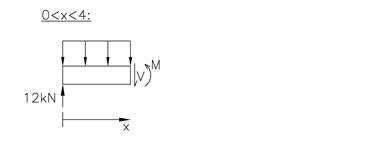
Vi tegner snittkreftene med positiv retning. For at V skal rotere elementet med klokken må V virke nedover. Momentet er tegnet slik at det gir strekk i underkant.

Skjærkraften skal være lik summen av ytre tverrkreftene:

Bøyemomentet skal være lik summen av ytre momenter om x:

Hvis vi tegner skjærkraftdiagrammet fra venstre mot høyre, starter vi med verdien 12kN i A pga. opplagerkraften A_i. V er, som vi ser av uttrykket over, rettlinjet mellom A og B og vi trenger en verdi ved B dvs. V(x = 4) =12 -8·4 = -20kN. Vi kan nå tegne resten av skjærkraftdiagrammet ved å følge kraftpilene.

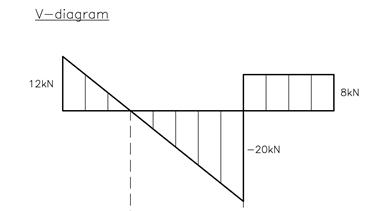
Mellom A og B blir bøyemomentet en parabel, jf. uttrykket over. I venstre ende hvor elementet er fritt opplagret får vi ikke noe bøyemoment. Vi må bestemme bøyemomentet ved B og vi må tallfeste bunnpunktet, dvs. der hvor V = 0.

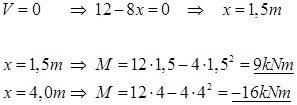
Nå kan vi tegne momentdiagrammet. Diagrammet er rettlinjet mellom B og C og har verdien null ved endene.

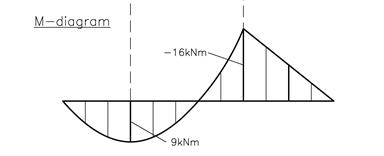
Hvis vi går tilbake til belastningsdiagrammet, så ser vi at vi kunne beregnet momentet i B langt enklere ved å gå fra høyre mot venstre; M_B = -8 ∙ 2 = -16.