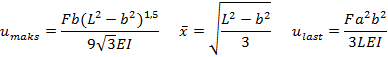I mekanikk er vi hovedsakelig interessert i å kontrollere om en konstruksjon er sterk nok til å bære de belastninger som virker på konstruksjonen uten å få varige deformasjoner. I noen tilfeller kan det også være nødvendig å beregne bjelkens elastiske utbøyning som følge av den ytre belastningen. Et eksempel kan være nedbøyningen av gulvbjelker når man står på et gulv. I tillegg til at gulvbjelken skal ha tilstrekkelig styrke, ønsker vi også at gulvet skal være behagelig å gå på og ikke gi etter når vi går. Krav som ikke relaterer seg direkte til styrke kan vi kalle for funksjonskrav. Vær obs på at også krav til utbøyning kan være utslagsgivende for valg av bjelkedimensjoner.

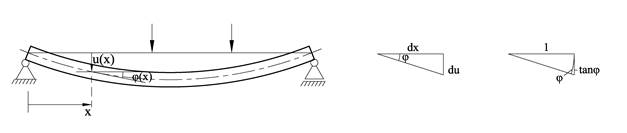
En rett bjelke som er utsatt for belastning på tvers vil bøyes slik at bjelkeaksen blir en krum kurve. Den utbøyde bjelkeaksens form kan uttrykkes ved utbøyningen u(x) og det er denne vi skal bestemme. Normalkrefter har ingen innflytelse på utbøyningen, og skjærkraft har minimal innflytelse, og vi ser derfor bort fra disse. Vi innfører størrelsen R som er nøytralaksens krumnings­radius. Uttrykket 1/R kalles for bjelkens krumning.

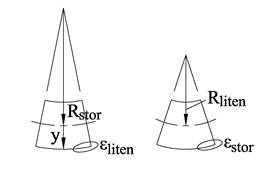
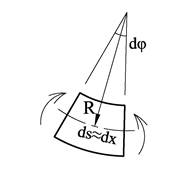
Jo mindre krumnings­­radius desto større blir tøyningen av materialet. Som vi tidligere har sett øker tøyningene lineært med avstanden til nøytralaksen og vi kan derfor sette opp uttrykket ε = y/R.

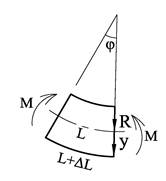
Med Hookes lov kan vi sette opp et uttrykk for bøyespenningene som funksjon av krumningen; σ = Ey/R. Ved å kombinere dette utrykket med bøyespenningsformelen finner vi sammenhengen mellom bjelkens krumning og bøyemomentet:

Uttrykket EI kalles for bjelkens bøyestivhet. Vi har altså funnet et uttrykk for krumningen, men målet er å bestemme utbøyningen. For alle praktiske formål kan vi forutsette at utbøyningene er svært små i forhold til geometrien for øvrig dvs. at u <<L; dermed kan vi forenkle beregningene en hel del. For små helningsvinkler blir φ » tan φ = du/dx. Videre kan vi anta at dx » ds. For små utbøyninger blir dermed 1/R lik den andrederiverte av utbøyningen:

Vi kan nå sette opp differensiallikningen for den elastiske linje:

Fortegnet i differensiallikningen skyldes at positivt moment gir en reduksjon i utbøyningen ved økende x. Vi husker at bøyemomentet er den integrerte av skjærkraften V som igjen er den integrerte av den fordelte lasten q. Dermed kan M(x) bestemmes ut fra bjelkens differensiallikning:

Bjelkens utbøyning kan altså bestemmes ved å løse differensiallikninger. Men punktlaster gir knekker i momentdiagrammet slik at krumningen M/EI ikke gis av en enkelt funksjon og dermed blir metodene for å løse slike differensiallikninger gjerne kompliserte og faller derfor utenfor pensum. Vi skal bruke resultatene direkte. Under følger de såkalte utbøyningsformlene som vi må kunne bruke.

Deformasjon av enkle bjelker

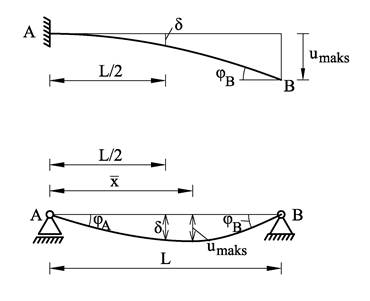
EI          = konstant

d            = utbøyning på midten

u_maks       = største utbøyning

u_last         = utbøyning under punktlast

x             = avstand fra A til punkt med maks. utbøyning

φ_A = φ_B = tangenthelning ved hhv. A og B

 

1
2
3
4
5
6
7

Overslagsberegning av utbøyning

Beregning av utbøyning for en fritt opplagret bjelke kan fort bli nokså omstendelig. Ved overslagsberegninger kan vi derfor bruke følgende formel hvor bjelkens største bøyemoment inngår:

Formelen kan brukes for enhver belastning og gir alltid større utbøyning enn den virkelige u_maks. Når vi regner på en slik måte at vi holder oss på den sikre siden sier vi at vi regner konservativt.

Statisk ubestemte problem

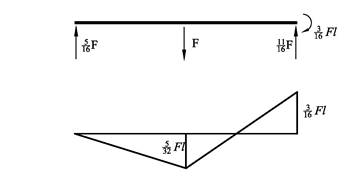
Vi kan også bruke nedbøyningsformlene til å bestemme opplagerkrefter for statisk ubestemte problem. Vi skal vise hvordan dette kan gjøres med et eksempel. Figuren viser en statisk ubestemt bjelke. Vi skal bestemme reaksjonskrefter og tegne momentdiagram for bjelken.

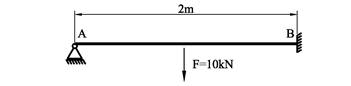
Nedbøyning i A som følge av F:

 

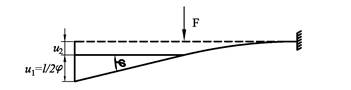
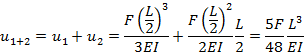
Oppbøyning i A som følge av F_A:

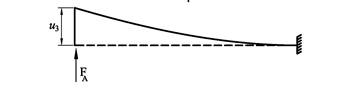
A skal verken opp eller ned dvs:

 

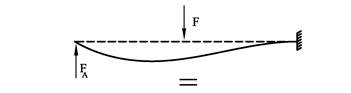
Vi har nå tre ukjente reaksjonskrefter som kan bestemmes vha. de vanlige likevektslikningene (ingen krefter i x-retning).

Setter opp belastningsdiagram og momentdiagram.