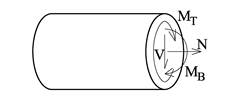
Ytre belastninger gir spenninger inni konstruksjonen og disse finner vi som spenningsresultanter eller snittkrefter dersom vi legger inn et tenkt snitt i konstruksjonen. Snittkreftene kan inndeles i aksialkraften N, bøyemomentet M_B, skjærkraften V og torsjonsmomentet M_T. Mens bøye­momentet M_B er et kraftpar pga normalspenninger som virker normalt på snittplanet er M_T et kraftpar pga skjær­spenninger som virker i snittplanet.

Vi har tidligere lært hvordan normalspenningene fra normalkraft og bøyemoment fordeler seg over bjelketverrsnittet;

σ_A =N/A

σ_B =(M_B/I_y)z

Vi skal nå se på hvordan skjærspenningene fordeler seg over tverrsnittet. Resultanten av skjærspenningene blir en kraft pluss et kraftpar i form av skjærkraften V og torsjonsmomentet M_T.

Torsjon

Med torsjon mener vi en vridning som følge av et moment som virker om elementets egen akse. Den første figuren viser forskjellen mellom torsjons­moment og bøyemoment som virker om en akse som ligger vinkelrett på elementaksen.

 

   

Vi kan f.eks. lage et torsjonsmoment ved å vi vri på staven med to vektstenger, og det påførte torsjonsmomentet blir M_T = Fa. Torsjon er først og fremst en problemstilling for akslinger og maskineri, og for tredimensjonale konstruksjoner. Vi skal se nærmere på hvordan skjær­spenningene som følge av torsjonsmoment fordeler seg over tverrsnittet, og vi begrenser oss til å se på sirkulære tverrsnitt. Figuren under viser et element som kun er utsatt for et torsjonsmoment.

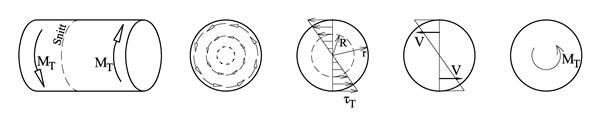
Vi ser at torsjonsskjærspenningene vokser proporsjonalt med avstanden fra tverrsnittets senter, og vi kan sette opp følgende uttrykk:

R er radien til det punktet hvor t_T skal bestemmes og I_P er det polare arealmoment. Vi er som regel interessert i å bestemme de største torsjonsskjærspenningene τ_T,maks, og disse finner vi ved ytterkanten dvs. ved R = r. Legg merke til at formelen for torsjonsskjærspenninger er nokså lik bøyespenningsformelen, men husk på at I_p ≠ I_x. Fra tabell på s. 46 i formelsamlingen kan vi hente følgende verdier for I_p.

 

Sirkulært massivt tverrsnitt:

Rør:

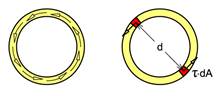
For tynnvegget rør kan vi anta at skjærspenningene varierer lite over godstykkelsen. Resultanten av τ skal være et kraftpar med momentet M_T, dermed kan vi utlede et forenklet uttrykk for torsjonsskjærspenningene:

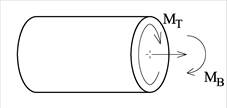
Torsjonsmoment er et kraftpar som virker om elementets x-akse mens bøyemomenter gjerne virker om bjelkens sterke y-akse eller svake z-akse. Vi kan derfor alternativt benevne M_T som M_x og M_B som M_y eller M_z.

Skjærspenninger pga skjærkraft

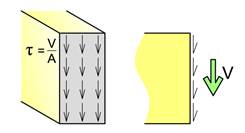
Skjærkraften V gir skjærspenninger τ i tverrsnittet og den enkleste måten å beregne skjærspenningene er å anta at disse fordeler seg jevnt over tverrsnittsarealet og virker i samme retning som skjærkraften. Da får vi en formel og et spenningsbilde som vist over. Det er vanlig å anta jevnt fordelte skjærspenninger for korte elementer som er utsatt for store skjærkrefter, såkalt klipping.

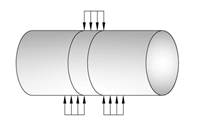
Flytegrensen som bestemmes av strekkprøveforsøk gjelder kun for normalspenninger σ. Når vi skal kontrollere skjærspenninger i forhold til flytning kan vi innføre en flyteskjærspenning som følger:

Legg merke til at skjærkapasiteten er langt lavere enn kapasiteten ved normalspenning. Dimensjoneringskriteriet for rene skjærepenninger blir da at de største skjærspenningene i elementet skal være mindre enn flyteskjærspenningen

Skjærspenninger som følge av bøyning

Styrken til en bjelke er ikke bare er avhengig av tverrsnittsprofilen, jf. figuren under. Dersom fibrene i materialet ikke henger sammen lik arkene i en bok så samvirker ikke materialet og det meste av profilets styrke forsvinner.

 

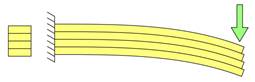
Dette skyldes at det ikke lenger overføres langsgående skjærkrefter mellom fibrene. Vi har følgende formel for å bestemme de langsgående, også kalt akseparallelle, skjærkreftene.

Som vi senere skal se er t_yx = t_xy jf. figuren under, og dermed kan vi også bestemme skjærspenningene på tverrsnittet.

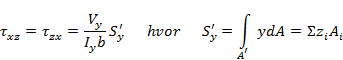
Formelen er litt spesiell og krever forklaring; det legges inn et langsgående snitt som deler tverrsnittet i to halvdeler og formelen gir oss da skjærspenningene som krysser denne linjen.  S’_y er arealmomentet flaten A’ som er den ene av de to halvdelene (fritt valgt halvdel). I_y er annet arealmoment av hele tverrsnittsarealet A. Både S’_y og I_y beregnes om y-aksen som går gjennom arealsenteret. Teorien sier ingenting om hvordan skjærspenningene fordeler seg over det langsgående snittet og man må derfor anta at skjærspenningene fordeler seg jevnt over snittet, derfor inneholder formelen b i nevneren som er snittets bredde. Jo tynnere tverrsnittets gods er ved snittet desto større blir derfor skjærspenningene. Egentlig gir formelen oss de langsgående skjærspenningene t_xz men disse er like store som t_zx som virker i snittet.

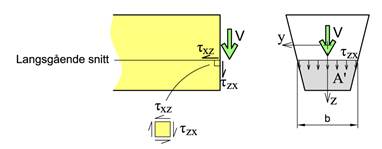
Forutsetningene for å bruke formelen er at den enkle bjelketeorien gjelder, dvs at bjelken ikke er veldig kort. Videre bør formelen bare brukes på snitt hvor skjærspenningene varierer lite over snittet; snittene bør derfor legges på tvers i forhold til godset. Formelen egner seg også best for tynnveggete profiler.

Eksempel

Bestem skjærspenninger i midten av tverrsnittet og ved posisjonen z / h/4 fra midten.

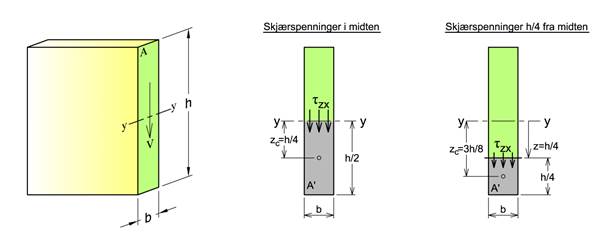
Skjærspenninger ved midten:

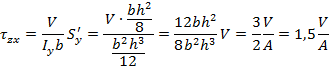
Ved posisjon z = h/4:

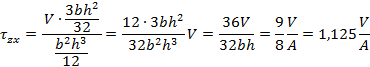
Skjærspenningsformelen kan være litt omstendelig og vi skal derfor konsentrere oss om resultatene fra formelen og se på hvordan skjær­spenningene fordeler seg over noen typiske tverrsnitt:

Rektangulært tverrsnitt

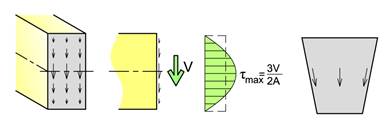
Legg merke til at t har samme retning som V og får en parabelform med sin største verdi ved arealsenteret, mens t er null i overkant og i underkant. t fordeler seg jevnt over bredden b og t følger typisk profilets konturer. Med skrå sider ville f.eks. t bli omtrent som vist på figuren til høyre.

Sirkulært tverrsnitt

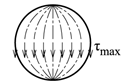
For sirkulære massive tverrsnitt blir skjærspenningsfordelingen nokså komplisert og vi begrenser oss til å sette opp et uttrykk for de største skjærspenningene.

Tynnvegget rør

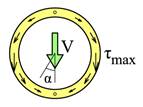
For tynnvegget rør følger skjærstrømmen godset i røret. Slik skjærkraften er påført får vi de største skjærspenningene på høyre og venstre side, mens skjærspenningene går til null oppe og nede.

Tynnvegget profil

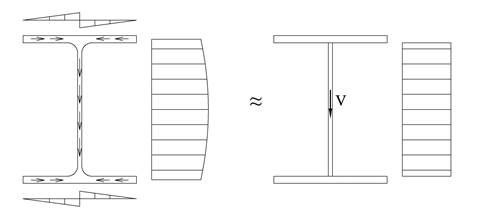
Skjærspenningene har konstant verdi over godstykkelsen og vi ser at skjærspenningene er parallelle med tverrsnittskonturene. Legg merke til at omtrent all skjærkraft overføres via steget. For H-bjelker er det som regel tilstrekkelig nøyaktig å regne at t kun virker i steget og fordeler seg jevnt over stegarealet A_s. Dermed kan vi sette opp:

For elementer hvor bjelkelengden L er vesentlig større enn bjelkehøyden h vil bøyespenningene typisk være langt større enn skjærspenningene, og som en tommelfingerregel kan man si at hvis L/h > 5 så ser vi bort fra tverrsnittskjærspenningene. Det kan likevel være fornuftig å foreta en overslagsberegning av t, spesielt for tynnveggede tverrsnitt. Heldigvis er det slik at de største skjærspenningene gjerne opptrer i midten mens de største bøyespenningene opptrer oppe og nede i tverrsnittet. Man bør imidlertid alltid gjøre en vurdering av om store skjærspenninger opptrer samme sted som de største bøyespenningene, og i så fall må vi undersøke det sammensatte spenningsbildet spesielt. Spesielt for høye og korte bjelker kan det være nødvendig å kontrollere kombinasjonen av t og s ved overgangen mellom steg og flens hvor både t og s er store.

For svært korte bjelker (L/h << 5) kan ikke den elementære bjelketeori brukes, og formlene over gjelder ikke. For bolter, skruer etc. antar man gjerne at skjærkraften fordeler seg jevnt over tverrsnittet, dvs. at τ =V/A.