Oppgave
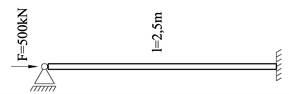
Figuren viser en søyle som er laget av et stangstål med diameter 60mm. Det benyttes konstruksjonsstål med kvalitet S355. Finn knekklast og knekkspenning.
Løsning
LK =0,7L = 1,75m
Bestemmer slankheten for å sjekke om vi får elastisk eller plastisk knekning.
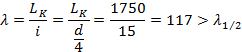
Vi er altså i det elastiske området.
![]()
![]()
Dvs. vi får elastisk knekking.
![]()
![]()
Vi ser at knekkspenningen ligger langt under flytegrensen.
Oppgave
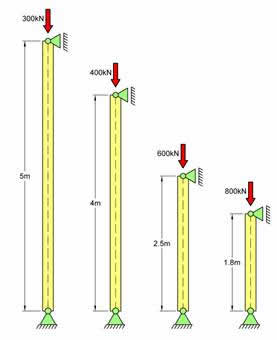
Dimensjoner fire søyler i forhold til knekking (HEA-bjelke). Sikkerhetsfaktor n = 2,0. Re = 355MPa
Løsning
|
Betegnelse |
A [mm2] |
Iz [mm4] |
iz [mm] |
|
HE100A |
2120 |
1,34·106 |
25,1 |
|
HE120A |
2530 |
2,31 “ |
30,2 |
|
HE140A |
3140 |
3,89 “ |
35,2 |
|
HE160A |
3880 |
6,16 “ |
39,8 |
|
HE180A |
4530 |
9,25 “ |
45,2 |
|
HE200A |
5380 |
13,4 “ |
49,8 |
|
HE220A |
6430 |
19,5 “ |
55,1 |
|
HE240A |
7680 |
27,7 “ |
60,0 |
![]()
Vi må vite om vi er i det plastiske eller elastiske området:
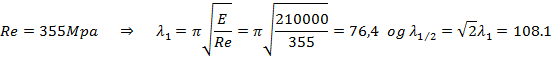
a) F = 300kN og LK = 5m
Vi antar at vi er i det elastiske området:
![]()
![]()
b) F = 400kN og LK = 4m
![]()
![]()
![]()
![]()
![]()
Ftillatt = FK/2,0 = 534kN > 400kN dvs HE180A er ok
c) F = 600kN og LK = 2,5m
![]()
Kortere bjelke betyr at knekking er ikke et så stort problem og det ser ut til at vi kan klare oss med en mindre bjelke til tross for mye større last.
Sjekker normalspenningene:
![]()
Prøver HE160A:
![]()
![]()
![]()
![]()
Ftillatt = FK/2,0 = 572kN < 600kN dvs HE160A er ikke ok
Prøver HE180A:
![]()
![]()
![]()
Ftillatt = FK/2,0 = 699kN > 600kN dvs HE180A er ok
Den forbedrede styrken skyldes hovedsakelig at økt tverrsnitt gir lavere spenninger men dels også at elementet blir mindre slank og dermed mindre utsatt for knekking
d) F = 800kN og LK = 1,8m
![]()
Prøver HE200A med A = 5380mm2 (Mulig at HE180A også kan brukes)
![]()
![]()
Hvis λ er mindre enn 20 så korrigerer vi ikke.
![]()
Ftillatt = FK/2,0 = 901kN > 800kN dvs HE200A er ok

