Oppgave
Figuren viser en fritt opplagret bjelke hvor det er benyttet IPE200. Beregn de største spenningene i bjelken.

Løsning
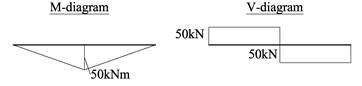
Vi beregner opplagerkrefter, tegner M- og V- diagrammer og finner Mdim=50kNm og Vdim=50kN som vi tar med oss i de videre beregningene.
Henter ut nødvendige tverrsnittsdata fra profiltabell og beregner de største bøyespenningene som vi finner i overkant og underkant av profilet:
![]()
Vi finner de største skjærspenningene midt på steget og beregner derfor arealmomentet av halve profilet. Her er det nyttig med en god figur
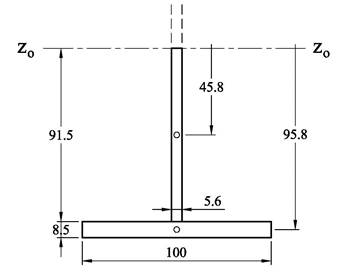
![]()
Beregner skjærspenningene:
![]()
Jevnføringsspenningen blir:
![]()
Den forenklede formelen for skjærspenninger gir en god tilnærming:
![]()
![]()
Den aktuelle bjelken har et lengde-høydeforhold L/h = 10, og vi ser at bøyespenningene er mer enn fem ganger større enn skjærspenningene. De største skjærspenningene opptrer ikke på samme stedet på tverrsnittet og skal derfor ikke kombineres. Til slutt ønsker vi å sjekke overgangen mellom steg og flens hvor vi har både skjærspenninger og normalspenninger.
![]()
![]()
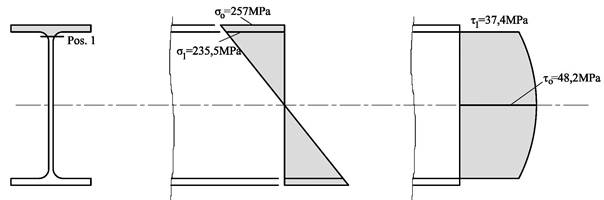
Vi har en-akset spenning og formelen for jevnføringsspenning blir:
![]()
Jevnføringsspenningene ved pos. 1 er mindre enn de største bøyespenningene og således ikke dimensjonerende.
Oppgave
I denne oppgaven skal vi kontrollere samme konstruksjon som i foregående eksempel, men denne gang skal det benyttes et T-profil hvor flensen er FB150x12 og steget er FB200x12. Stålkvalitet er S355.
Løsning
Fra foregående eksempel har vi funnet Mdim = 50kNm under punktlasten. Videre har vi skjærkraften V = 50kN gjennom hele bjelken. Vi begynner med å beregne tverrsnittsegenskaper:
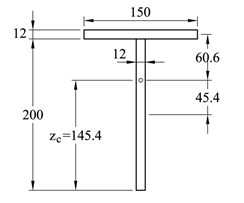
Arealsenter:
![]()
Beregner arealmoment om y-aksen for den del av steget som er under y-aksen og for hele steget.
![]()
![]()
Annet arealmoment om tverrsnittets y-akse:
![]()
Beregner skjærspenninger i steget
![]()
![]()
Skjærspenningen blir omtrent som følger.
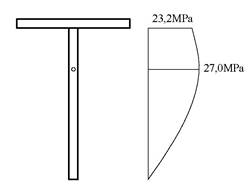
Dersom vi fordeler skjærkraften jevnt over steget får vi for lave spenninger og dette er derfor en uegnet forenkling for T-profiler:
![]()
Beregner jevnføringsspenninger i arealsenteret:
![]()
Beregner til slutt de største normalspenninger:
![]()
Flytegrensen overskrides dvs. ikke ok.
Oppgave
Et rør med dimensjon Ø193,7x6,0 er belastet med torsjonsmomentet MT = 20kNm og aksiallasten Fx = 150kN. Beregn sikkerhet i forhold til flyt for materialet. Flytegrensen er σ = 235MPa.
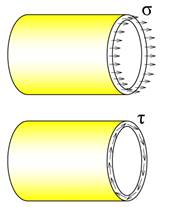
Løsning
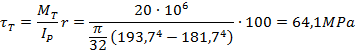
![]()
![]()
![]()
Oppgave
Figuren viser en fritt opplagret bjelke hvor det er benyttet FB100x6, og vi skal se nærmere på spenningene rett under punktlasten F. Vi må først ta stilling til hvor stor flate punktlasten skal fordeles over. Vi har lite opplysninger og vi antar derfor at punktlasten fordeler seg over et kvadrat med dimensjoner 6×6 = 36mm2.
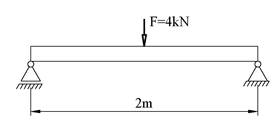
Løsning
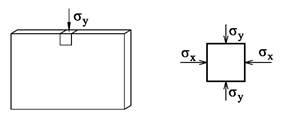
Vi får normalspenninger σx i lengderetningen pga bøying:
![]()
![]()
Vi får normalspenninger σy på tvers pga kontakttrykket:
![]()
Kombinerer σx og σy vha. jevnføringsspenningen:
![]()
Som vi ser reduserer σy jevnføringsspenningen og i dette tilfellet vi det neppe være aktuelt å ta hensyn til tverrspenningen i dimensjoneringssammenheng.
Oppgave
Figuren viser en veivaksel som er belastet med kraften 400kN på veiva. Beregn de største skjærpenninger, normalspenninger og jevnføringsspenninger i akselen.
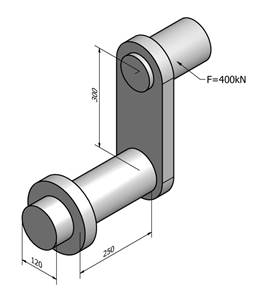
Løsning
Figuren viser hvor vi finner de største spenningene
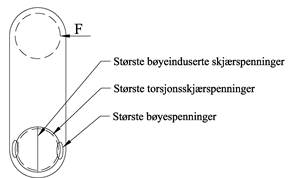
Torsjonsskjærspenninger
![]()
![]()
![]()
Disse befinner seg på hele overflaten til akselen.
Skjærspenninger pga bøyning
![]()
Disse befinner seg på et vertikalt plan midt inni akselen. Legg merke til at vi har ett punkt hvor både τT og τV virker i samme retning og vi kan legge disse sammen uten videre.
![]()
![]()
Normalspenninger fra bøyemoment
MB = 400·0,25 = 100kNm
![]()
![]()
Disse finner vi oppe og nede, ved opplageret. Her har vi også torsjonsskjærspenninger og jevnføringsspenningene blir:
![]()

