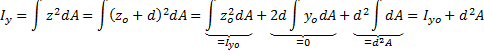Flategeometri

Areal, arealsenter og arealmoment

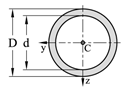
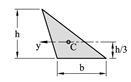
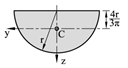
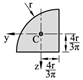
På tilsvarende vis som vi finner tyngde og tyngdepunkt til et legeme kan vi bestemme areal og arealsenter til todimensjonale flater. Figurene under viser formler for arealet og beliggenhet for arealsenteret for noen enkle geometriske flater. Legg spesielt merke til avstanden h/3 for trekantete flater og 4r/3π for halv- og kvartsirkelen.

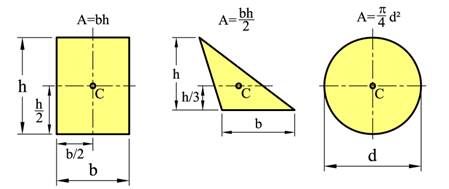
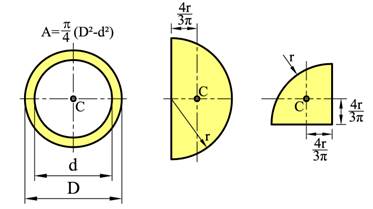
Beregning av areal og arealsenter er et nyttig hjelpemiddel når vi skal bestemme resultanten av parallelle krefter. Vi kan også benytte arealer for å gjøre fordelte laster om til punktlaster, når vi beregner tyngde og tyngdepunkt for legemer, og når vi skal finne sammenhenger mellom spenninger og snittkrefter. Vi skal her se hvordan areal og arealsenter bestemmes, uavhengig av anvendelsesområdet.

                  

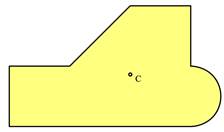
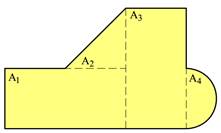
Når vi skal finne arealet av en sammensatt flate, deles flaten i et antall delflater med enkel geometri og flatens totale areal finner vi ved å legge sammen delarealene, dvs. A_TOT = ΣA_i. Når vi skal finne arealsenterets beliggenhet må vi velge oss et referansepunkt og vi må innføre et koordinatsystem hvor vi orienterer f.eks. x- og y-aksen i forhold til geometrien.

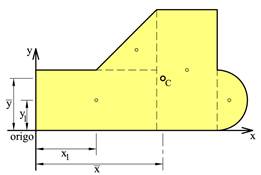
Arealsenteret er definert som følger:

S_y og S_x er “første arealmoment” om henholdsvis y-aksen og x-aksen. Formlene forutsetter at vi kan dele flaten inn i et endelig antall deflater. Dersom dette ikke er tilfelle må vi integrere og formlene for areal og arealsenter blir som følger:

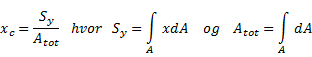
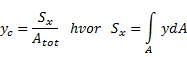
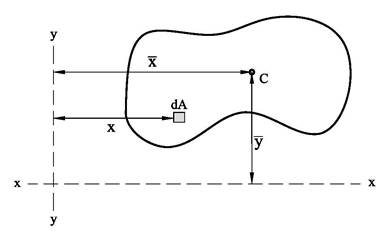
Annet arealmoment

En annen geometrisk størrelse som står sentralt i mekanikk er “annet arealmoment”  som er definert som følger:

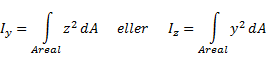
Første arealmoment S_y og annet arealmoment I_y har helt forskjellige egenskaper og anvendelsesområder og må ikke forveksles. Annet arealmoment er et matematisk hjelpemiddel som uttrykker hvordan arealet er fordelt i forhold til en akse. Annet arealmoment får enheten mm⁴. Et annet navn for annet arealmoment er arealtreghetsmomentet.

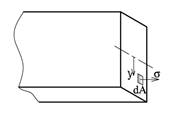
Når annet arealmoment skal bestemmes må vi integrere over en flate, typisk et bjelketverrsnitt. I uttrykket for I_y inngår z² hvor z er avstanden til y-aksen, og på tilsvarende vis inngår y² i I_z hvor y er avstanden til z-aksen. Annet arealmoment kan beregnes om enhver akse så lenge aksen ligger i flatens plan, og det er i utgangspunktet opp til oss å definere orienteringen på y-aksen og z-aksen. Vi bør derfor angi hvilken akse annet arealmoment refererer til; I_y betyr f.eks. ”annet arealmoment om y-aksen” hvor y-aksen går gjennom flatens arealsenter. Annet arealmoment påvirkes i stor grad av aksens orientering og beliggenhet. I mekanikk beregnes annet arealmoment alltid om en akse som går gjennom arealsenteret og y- og z-aksenes orientering sammenfaller typisk med flatens geometriske utforming og hvordan disse typisk brukes.

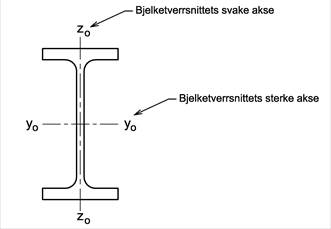
I bøyespenningsformelen må vi beregne annet arealmoment av bjelkens tverrsnittsareal om den aksen som bjelken bøyes om, og denne aksen skal gå gjennom tverrsnittets arealsenter (vi bruker y og z om disse aksene). Figuren viser de to viktigste aksene for en typisk bjelkeprofil. I_yo brukes for bjelker som bøyes om profilets sterke akse mens I_zo brukes ved bøyning om profilets svake akse.

Beregning av annet arealmoment

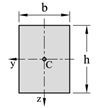
Annet arealmoment er definert ved integrasjonsuttrykk og for flater med enkel geometri kan man utlede eksakte uttrykk for I_y og I_z som vi finner i formelsamlinger. Vi skal se hvordan vi kan bestemme annet arealmoment for en rektangulær flate. Arealmomentet regnes om y-aksen som går gjennom arealsenteret og som er orientert slik figuren under viser.

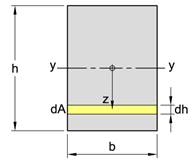
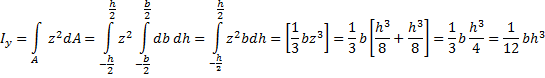
Legg merke til at høyden har svært stor innvirkning på annet arealmoment mens arealmomentet vokser proporsjonalt med flatens bredde. Uttrykket bh³/12 er et viktig resultat som vi skal bruke mye i fasthetslæren. Tabellen under viser de viktigste uttrykkene for annet arealmoment om y- og z-akser som går gjennom arealsenteret.

Snittflate	Areal	Annet arealmoment	Tverrsnittsmodul	Polart arealmoment
			-	-
			-	-
			-	-

For standardprofiler kan annet arealmoment hentes fra såkalte profiltabeller som vi finner i håndbøker og formelsamlinger.

Steiners formel

Når vi skal bestemme annet arealmoment av flater med komplisert geometri, f.eks. tverrsnittet til H-bjelker, vinkelprofiler og liknende, deles flaten inn i delflater med enkel geometri. Annet arealmoment beregnes for hver delflate og disse legges sammen, dvs. I_y = I_y1 + I_y2 osv.

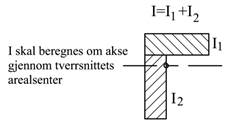
Nå er det slik at formlene i tabellen over ikke kan brukes direkte fordi disse gir oss annet arealmoment for akser gjennom delflatens arealsenter mens annet arealmoment skal beregnes om aksen gjennom hele flatens arealsenter. mens For delflate i gir formelen I_yoi = bh³/12 annet arealmoment om delflatens eget arealsenter mens I_yi skal beregnes om en y-akse som går gjennom hele flatens arealsenter.

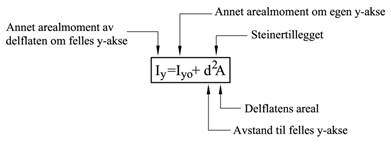
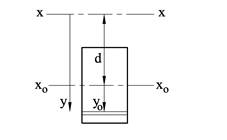
Steiners formel brukes for å bestemme økningen i annet arealmoment når momentaksen parallellforskyves bort fra arealsenteret. Formelen inneholder to ledd; første ledd er annet arealmoment om y_o-aksen gjennom flatens arealsenter (typisk bh³/12) og andre ledd d²A er økningen i annet arealmoment som følge av at aksen parallellforskyves. d er avstanden mellom de to aksene og A er flatens areal. Legg merke til at siden avstanden d kvadreres vil “steinertillegget” alltid være positivt. I_yo om akse gjennom arealsenteret vil således være det minste annet arealmoment vi kan ha.

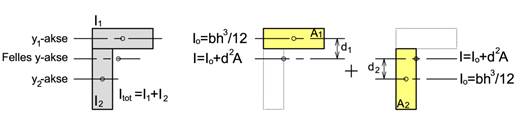
For hver delflate bestemmes areal (typisk A = b·h) og annet arealmoment om egen akse (typisk I = bh³/12). Avstanden mellom lokalt arealsenter og felles arealsenter må også bestemmes og alt dette må settes sammen til annet arealmoment:

Steiners formel kan utledes som følger. Figuren under viser en flate hvor vi skal beregne I_x om en vilkårlig akse x-x, og denne aksen har avstanden d i forhold til aksen x_o – x_o gjennom arealsenteret. Vi får da