Oppgave

Figuren viser en bjelke av typen FB200x20 som er belastet som vist. Kontroller spenningene i bjelken. Største tillatte spenninger s_tillatt = 200MPa.

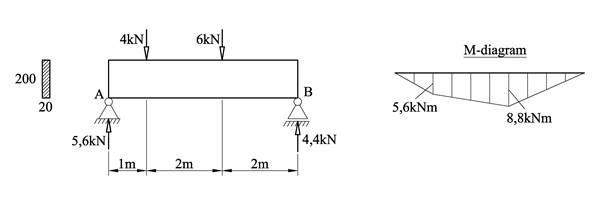
Løsning

Vi starter med å beregne opplagerkreftene, deretter bøyemomentet under punktlastene og tegner så opp bøyemomentdiagram som vist over.

 

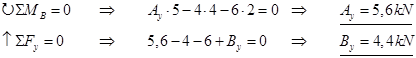
Vi henter ut det største bøyemomentet M_dim = 8,8kNm fra diagrammet.

Annet arealmoment for FB200x20:

Største normalspenninger:    dvs. OK

Oppgave

Figuren viser en fritt opplagret IPE140 stålprofil med R_e = 235MPa. Kontroller bjelken i forhold til flyt når sikkerhetsfaktoren skal være minst n = 2,0.

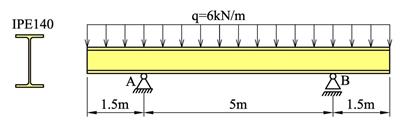
Løsning

Symmetri tilsier at hvert opplager tar halve lasten dvs. F_Ay = F_By = 6·8/2=24kN. Setter opp uttrykk for snittkreftene mellom A og B:

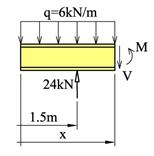
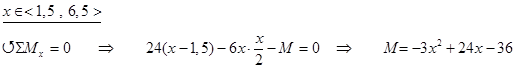
Finner beliggenheten til topp- og bunnpunkt ved å derivere uttrykket over:

Regner ut verdier for momentdiagrammet ved opplagrene og ved midten:

 

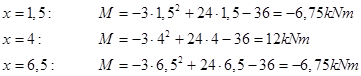
På tilsvarende vis kan man sette opp uttrykk for M for de deler av bjelken som er utenfor opplagrene. Men vi vet at M=0 ved endene, vi kjenner momentet ved opplagrene og vi vet hvilken kurvatur momentdiagrammet skal ha. Dermed har vi nok opplysninger til å tegne momentdiagrammet.

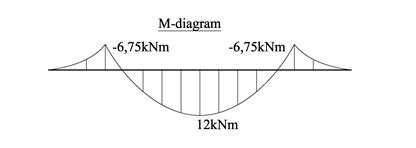
Momentdiagrammet er symmetrisk og diagrammet er tegnet på strekksiden. Det største opptredende bøyemomentet for bjelken er M_dim=12kNm og vi tar denne med oss i de videre beregningene.

 

Fra profiltabellen henter vi annet arealmoment I_y = 541cm⁴ for IPE140. Vi får største opptredende spenninger i overkant og underkant:

Prøver IPE160 med I = 869cm⁴:

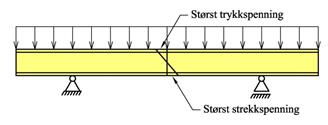
Figuren under viser hvor vi finner de største spenningene.

 

Oppgave

Bestem de største normalspenningene i konstruksjonen hvis vi (1) velger rør Ø200x8 eller (2) T140-profil

Løsning

Bestemmer opplagerkrefter som presenteres i belastningsdiagram og så tegner vi diagram for de tre snittkreftene V, M og N.

 

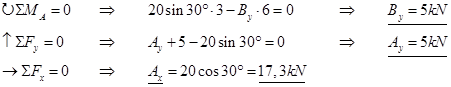
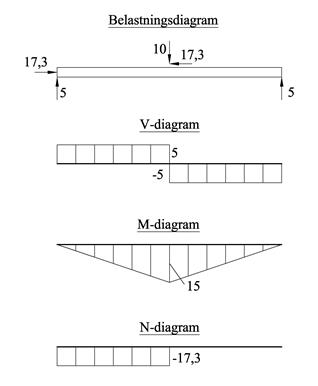
Vi finner det største bøyemomentet midt på bjelken. Hvis vi ser på et snitt like til venstre for midten, får vi dessuten en aksialkraft. Bruker derfor M_dim = 15kNm og N_dim = -17,3kN.

(1)  Rør 200x8

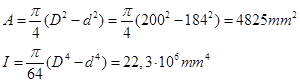
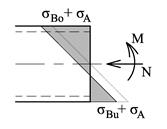
Tegner en skisse som viser spenningene i tverrsnittet. Areal­senteret ligger i midten og bøyemomentet gir derfor like store bøyespenninger i overkant og i underkant (men motsatt rettet). På oversiden gir både σ_B og σ_A trykk og disse forsterker hverandre. Vi finner altså de største spenningene i overkant

 

(2)   T140:

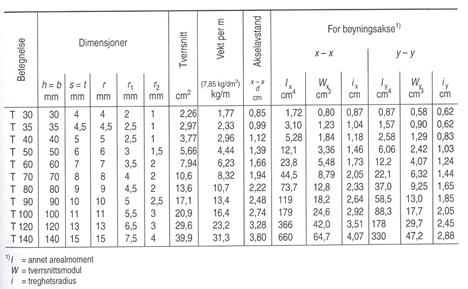
Fra profiltabell henter vi følgende tverrsnittsdata: A = 3990mm², I_x = 6,6·10⁶mm⁴, d = 38mm

 

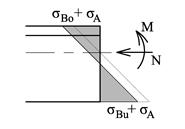
Tegner en skisse av spenningene. I og med at arealsenteret ligger nærmest overkanten vil vi få størst bøyespenninger i underkant (strekk). I dette tilfellet bør vi ikke redusere σ_Bu med σ_A. Husk på at like til høyre for midten har vi ingen aksialkraft. På oversiden derimot hvor både σ_Bo og σ_A gir trykk bør vi korrigere (dvs vi ser på venstre siden av midten). Det kan være vanskelig å vurdere hvor vi får de største spenningene og vi sjekker for ordens skyld både i overkant og i underkant.

    og   

Legg merke til σ_A som er langt mindre enn σ_B og dette er typisk.