Oppgave

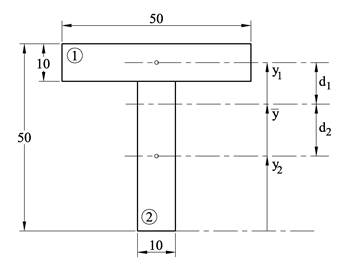
Figuren viser et T-profil som er bygget av to stk. flattstål. Beregn annet arealmoment om tverrsnittets sterke akse.

 

Løsning

Deler tverrsnittet inn i to delflater og velger en referanselinje i underkant.

Delflate 1	Delflate 2	Tverrsnitt
A1 = 500mm2	A2 = 400mm2	ATOT = A1 + A2 = 900mm2
z1 = 45mm	z2 = 20mm	zc = (500·45+400·20)/900 = 33,9mm
d1 = 45-33,9 = 11,1mm	d2 = 33,9 – 20 = 13,9mm

Delflate 1:

Delflate 2:

Tverrsnittet

 Legg merke til at for flensen så er den lokale I liten mens steinertillegget d2A er stort. Flensen er altså ikke særlig sterk i seg selv, det er først når den flyttes vekk fra nøytralaksen at den gir et skikkelig bidrag. Til slutt tar vi med hvordan motstandsmoment for tverrsnittet bestemmes. Vi tar bare med minste motstandsmoment dvs. W_yu.

Oppgave

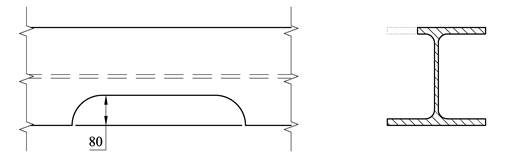
Figuren viser en bjelke av typen HE260B hvor det er gjort et utkapp i den ene flensen. Beregn annet arealmoment for det reduserte tverrsnittet.

Løsning

Dette eksemplet viser hvordan annet arealmoment kan beregnes når vi tar bort areal, og hvordan vi kan kombinere verdier fra profiltabeller med håndberegninger. Vi tenker oss at det intakte profilet er sammensatt av to delflater, og så regner vi oss bakover til vi finner annet arealmoment for flate 2.

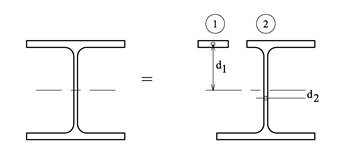
Intakt tverrsnitt (fra tabell):

A = 118cm², I_y = 14920cm⁴

Delflate 1:

A₁ = 8×1,75 = 14cm², d₁ = 13 – 0,875 = 12,125cm

Delflate 2:

A₂ = 118 – 14 = 104cm², I₂ = 14920 – 2062 = 12858,2cm⁴

Annet arealmoment beregnet over refererer til arealsenteret for det intakte tverrsnittet, men for det reduserte tverrsnitt vil arealsenteret flytte seg nedover. Vi beregner arealsenterets nye beliggenhet i forhold til midten av det intakte profilet og får:

Bruker til slutt Steiners formel for å regne oss tilbake til I₀₂ som er annet arealmoment for det reduserte tverrsnitt om tverrsnittets eget arealsenter.